Tutorial: Reducing a heat equation using balanced truncation

Heat equation

We consider the following one-dimensional heat equation over \((0, 1)\) with two inputs \(u_1, u_2\) and three outputs \(y_1, y_2, y_2\):

\[\begin{split}\begin{align} \partial_t T(\xi, t) & = \partial_{\xi \xi} T(\xi, t) + u_1(t), & 0 < \xi < 1,\ t > 0, \\ -\partial_\xi T(0, t) & = -T(0, t) + u_2(t), & t > 0, \\ \partial_\xi T(1, t) & = -T(1, t), & t > 0, \\ y_1(t) & = T(0, t), & t > 0, \\ y_2(t) & = T(0.5, t), & t > 0, \\ y_3(t) & = T(1, t), & t > 0. \end{align}\end{split}\]

In the following, we will create a discretized Model and reduce it using the balanced truncation method to approximate the mapping from inputs \(u = (u_1, u_2)\) to outputs \(y = (y_1, y_2, y_3)\).

Discretized model

We need to construct a linear time-invariant (LTI) system

\[\begin{split}\begin{align} E \dot{x}(t) & = A x(t) + B u(t), \\ y(t) & = C x(t) + D u(t). \end{align}\end{split}\]

In pyMOR, these models are captured by LTIModels from the pymor.models.iosys module.

There are many ways of building an LTIModel. Here, we show how to build one from custom matrices instead of using a discretizer as in Tutorial: Using pyMOR’s discretization toolkit and the to_lti of InstationaryModel. In particular, we will use the from_matrices method of LTIModel, which instantiates an LTIModel from NumPy or SciPy matrices.

First, we do the necessary imports.

import matplotlib.pyplot as plt
import numpy as np
import scipy.sparse as sps
from pymor.models.iosys import LTIModel
from pymor.reductors.bt import BTReductor

Next, we can assemble the matrices based on a centered finite difference approximation:

k = 50
n = 2 * k + 1

A = sps.diags(
    [(n - 1) * [(n - 1)**2], n * [-2 * (n - 1)**2], (n - 1) * [(n - 1)**2]],
    [-1, 0, 1],
    format='lil',
)
A[0, 0] = A[-1, -1] = -2 * n * (n - 1)
A[0, 1] = A[-1, -2] = 2 * (n - 1)**2
A = A.tocsc()

B = np.zeros((n, 2))
B[:, 0] = 1
B[0, 1] = 2 * (n - 1)

C = np.zeros((3, n))
C[0, 0] = C[1, k] = C[2, -1] = 1

Then, we can create an LTIModel:

fom = LTIModel.from_matrices(A, B, C)

We can get the internal representation of the LTIModel fom

fom

LTIModel(
    NumpyMatrixOperator(<101x101 sparse, 301 nnz>, source_id='STATE', range_id='STATE'),
    NumpyMatrixOperator(<101x2 dense>, range_id='STATE'),
    NumpyMatrixOperator(<3x101 dense>, source_id='STATE'),
    D=ZeroOperator(NumpyVectorSpace(3), NumpyVectorSpace(2)),
    E=IdentityOperator(NumpyVectorSpace(101, id='STATE')))

From this, we see that the matrices were wrapped in NumpyMatrixOperators, while default values were chosen for \(D\) and \(E\) matrices (respectively, zero and identity). The operators in an LTIModel can be accessed directly, e.g., fom.A.

We can also see some basic information from fom’s string representation

print(fom)

LTIModel
    class: LTIModel
    number of equations: 101
    number of inputs:    2
    number of outputs:   3
    continuous-time
    linear time-invariant
    solution_space:  NumpyVectorSpace(101, id='STATE')

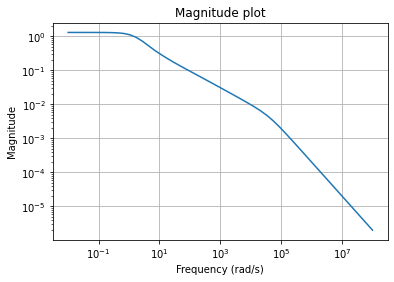
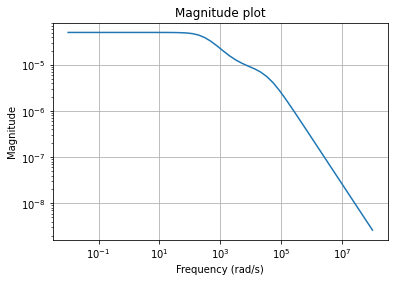
To visualize the behavior of the fom, we can draw its magnitude plot, i.e., a visualization of the mapping \(\omega \mapsto H(i \omega)\), where \(H(s) = C (s E - A)^{-1} B + D\) is the transfer function of the system.

w = np.logspace(-2, 8, 50)
fom.mag_plot(w)
plt.grid()
_images/tutorial_bt_6_0.png

Plotting the Hankel singular values shows us how well an LTI system can be approximated by a reduced-order model

hsv = fom.hsv()
fig, ax = plt.subplots()
ax.semilogy(range(1, len(hsv) + 1), hsv, '.-')
ax.set_title('Hankel singular values')
ax.grid()
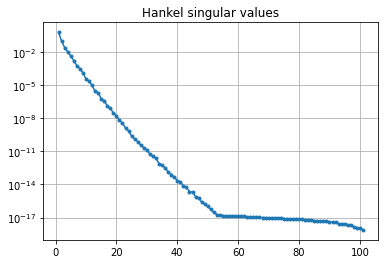
_images/tutorial_bt_7_0.png

As expected for a heat equation, the Hankel singular values decay rapidly.

Running balanced truncation

The balanced truncation method consists of finding a balanced realization of the full-order LTI system and truncating it to obtain a reduced-order model. In particular, there exist invertible transformation matrices \(T, S \in \mathbb{R}^{n \times n}\) such that the equivalent full-order model with \(\widetilde{E} = S^T E T = I\), \(\widetilde{A} = S^T A T\), \(\widetilde{B} = S^T B\), \(\widetilde{C} = C T\) has Gramians \(\widetilde{P}\) and \(\widetilde{Q}\), i.e., solutions to Lyapunov equations

\[\begin{split}\begin{align} \widetilde{A} \widetilde{P} + \widetilde{P} \widetilde{A}^T + \widetilde{B} \widetilde{B}^T & = 0, \\ \widetilde{A}^T \widetilde{Q} + \widetilde{Q} \widetilde{A} + \widetilde{C}^T \widetilde{C} & = 0, \\ \end{align}\end{split}\]

such that \(\widetilde{P} = \widetilde{Q} = \Sigma = \operatorname{diag}(\sigma_i)\), where \(\sigma_i\) are the Hankel singular values. Then, taking as basis matrices \(V, W \in \mathbb{R}^{n \times r}\) the first \(r\) columns of \(T\) and \(S\) (possibly after orthonormalization), gives a reduced-order model

\[\begin{split}\begin{align} \widehat{E} \dot{\widehat{x}}(t) & = \widehat{A} \widehat{x}(t) + \widehat{B} u(t), \\ \widehat{y}(t) & = \widehat{C} \widehat{x}(t) + D u(t), \end{align}\end{split}\]

with \(\widehat{E} = W^T E V\), \(\widehat{A} = W^T A V\), \(\widehat{B} = W^T B\), \(\widehat{C} = C V\), which satisfies the \(\mathcal{H}_\infty\) (i.e., induced \(\mathcal{L}_2\)) error bound

\[\sup_{u \neq 0} \frac{\lVert y - \widehat{y} \rVert_{\mathcal{L}_2}}{\lVert u \rVert_{\mathcal{L}_2}} \leqslant 2 \sum_{i = r + 1}^n \sigma_i.\]

Note that any reduced-order model (not only from balanced truncation) satisfies the lower bound

\[\sup_{u \neq 0} \frac{\lVert y - \widehat{y} \rVert_{\mathcal{L}_2}}{\lVert u \rVert_{\mathcal{L}_2}} \geqslant \sigma_{r + 1}.\]

To run balanced truncation in pyMOR, we first need the reductor object

bt = BTReductor(fom)

Calling its reduce method runs the balanced truncation algorithm. This reductor additionally has an error_bounds method which can compute the a priori \(\mathcal{H}_\infty\) error bounds based on the Hankel singular values:

error_bounds = bt.error_bounds()
fig, ax = plt.subplots()
ax.semilogy(range(1, len(error_bounds) + 1), error_bounds, '.-')
ax.semilogy(range(1, len(hsv)), hsv[1:], '.-')
ax.set_xlabel('Reduced order')
ax.set_title(r'Upper and lower $\mathcal{H}_\infty$ error bounds')
ax.grid()
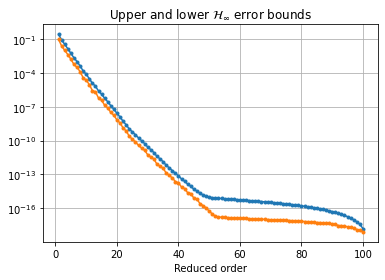
_images/tutorial_bt_9_1.png

To get a reduced-order model of order 10, we call the reduce method with the appropriate argument:

rom = bt.reduce(10)

Instead, or in addition, a tolerance for the \(\mathcal{H}_\infty\) error can be specified, as well as the projection algorithm (by default, the balancing-free square root method is used). The used Petrov-Galerkin bases are stored in bt.V and bt.W.

We can compare the magnitude plots between the full-order and reduced-order models

fig, ax = plt.subplots()
fom.mag_plot(w, ax=ax, label='FOM')
rom.mag_plot(w, ax=ax, linestyle='--', label='ROM')
ax.legend()
ax.grid()
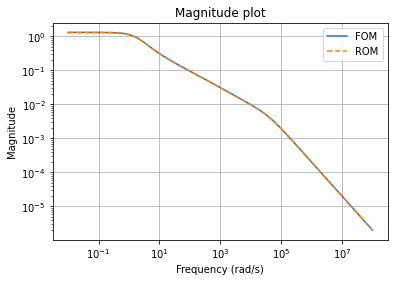
_images/tutorial_bt_11_0.png

and plot the magnitude plot of the error system

(fom - rom).mag_plot(w)
plt.grid()
_images/tutorial_bt_12_0.png

We can compute the relative errors in \(\mathcal{H}_\infty\) or \(\mathcal{H}_2\) (or Hankel) norm

print(f'Relative Hinf error: {(fom - rom).hinf_norm() / fom.hinf_norm():.3e}')
print(f'Relative H2 error:   {(fom - rom).h2_norm() / fom.h2_norm():.3e}')

Relative Hinf error: 3.702e-05
Relative H2 error:   6.399e-04

Note

To compute the \(\mathcal{H}_\infty\) norms, pyMOR uses the dense solver from Slycot, and therefore all of the operators have to be converted to dense matrices. For large systems, this may be very expensive.

Download the code: tutorial_bt.py tutorial_bt.ipynb